Contents
Everything you need to know about Virtual Cement
[wpecpp name=”package” price=”75″ align=”center”]
by Jeffrey W. Bullard*, Clarissa Ferraris*, Edward J. Garboczi*, Nicos Martys*, and Paul Stutzman*
Cementitious materials, including cement paste, mortar, and concrete, possess great chemical and structural complexity. Chemically, cement pastes contain many chemical components and mineral phases. Many of these phases can be amorphous or poorly crystalline, with metastable solid solution compositions varying over a fairly wide range. Dozens of chemical hydration reactions may occur simultaneously at rates that vary from region to region within the material. Structurally, a cementitious material is a random composite structure on length scales from nanometers to millimeters, and the contrast in various physical properties among the different composite phases is often quite large. One would be hard pressed to find a system that even approaches this range of complexity from among other classes of engineering materials such as ceramics and metals.
One consequence of this complexity is that the hydration, properties, and long-term field perform-ance of cement and concrete are difficult to predict; simple empirical relations cannot be universally applied with confidence. As a result, mix design and optimization for tailored applications is a long, arduous, and expensive proposition.
A promising alternative is to use scientifically based models to guide testing and development efforts. To be accurate and reliable, such models must account for all the relevant chemistry and physics that influence cementitious systems. Because of the complexity of these materials, these models must take the form of computer simulations. Computer hardware has advanced to the point that sufficient computational power for most relevant simulations can be obtained on a standard personal desktop computer. Therefore, computer modeling potentially could supplant much of the current empirical design and testing procedures with relatively inexpensive and quick simulations. Computer modeling applied to materials is usually called “computational materials science,” which is a term that will be used extensively throughout this chapter. What is meant by “computational materials science of concrete” is this: computer-based models of microstructure at the relevant length scale, operated on by algorithms that give accurate measures of physical properties.
THE COMPUTATIONAL MATERIALS SCIENCE OF CEMENT AND CONCRETE: A BRIEF HISTORY
It is important to know from where the ideas behind the computational materials science of concrete came. There were four main intellectual sources for these ideas. First is the work on the structure of amorphous semiconductors like silicon and germanium in the 1960s and 1970s.
Physicists could do crystal physics calculations on periodic crystals; however, the problem of amor-phous semiconductors was entirely different. If there was no underlying crystal lattice, how was one to do any calculations at all? Analytical approximations were tried, with only a limited degree of success (Zallen, 1983). Then models were built, where several hundred atoms were represented by a computer simulation model. Algorithms were applied to these models to compute properties, which were then used in an attempt to explain experimental results.
The second and third sources were two highly innovative developments in the materials science of concrete community, both in the 1980s, which appeared to be unrelated to the previous amor-phous semiconductor work, but which in fact were similar to it. Wittmann, Roelfstra, and Sadouki published two important papers on numerically simulating the structure and properties of concrete in 2-D (Wittmann and others, 1984; Roelfstra and others, 1985). Simple models were developed for simulating the shape and arrangement of aggregates in concrete. A finite element grid was applied to these models in order to compute properties like thermal conductivity and elastic moduli.
Then, independently, Jennings and Johnson published work on a three-dimensional (3-D) model of cement paste microstructure development for C3S pastes (Jennings and Johnson, 1986). This effort carried the development of computational materials science down to the micrometer scale of cement. Various sized particles, which followed a real cement particle size distribution, were dispersed randomly in 3-D. Rules were applied to these continuum spherical particles to simulate the dissolution of cement and the growth of hydration products.
The fourth intellectual source was a paper showing how a random walk algorithm could be applied to continuum models to compute electrical and diffusive transport in their pore space (Schwartz and Banavar, 1989). While trying to apply this algorithm to Jennings’ cement paste model, since it was a continuum model, we experimented with digitizing the microstructure of simple models and then using random walks on the digital lattice. The combination of the ideas of random walks, digital images, and a cement paste hydration microstructure development model led directly to the first NIST cement paste hydration model. The subsequent realization that any finite element or finite difference algorithm would work on a digital lattice allowed almost any physical property to be computed and so greatly increased the ability of the cement paste model to produce predictions that were directly comparable to experimental results.
It should be mentioned that other kinds of random structure models grew popular around the same time, like the diffusion-limited aggregation (Meakin, 1988) and Eden models (Eden, 1961). All these kinds of models have similarities, except that actual cement chemistry is built into the cement hydration model. These other two models are examples of rule-based or cellular automa-ton models where the rules are chosen somewhat arbitrarily, and not always in close company with some known physics or chemistry (Wolfram, 1986; Young and Corey, 1990), even though physically realistic behavior is often seen.
THE VIRTUAL CEMENT AND CONCRETE TESTING LABORATORY
The computational materials science of cement and concrete has been an active research area at NIST since the early 1980s, in close synergy with experimental materials science. A wide range of computational tools has been developed to model microstructure, simulate hydration, and calcu-late physical properties. This digital “tool-kit” (Garboczi and others, 1999) includes programs for simulating cement hydration and building three-dimensional cement paste microstructures, assembling three-dimensional concrete microstructures using model aggregates, analyzing microstructures using percolation concepts, and computing physical (thermal, electrical, diffu-sional, and mechanical) properties using finite difference, finite element, and random walker algo-rithms. These are all described in an “Electronic Monograph,” which is a web-based book of well over 2000 pages used by an average of 9000+ users per month from 80+ countries (Garboczi and others, 1997).
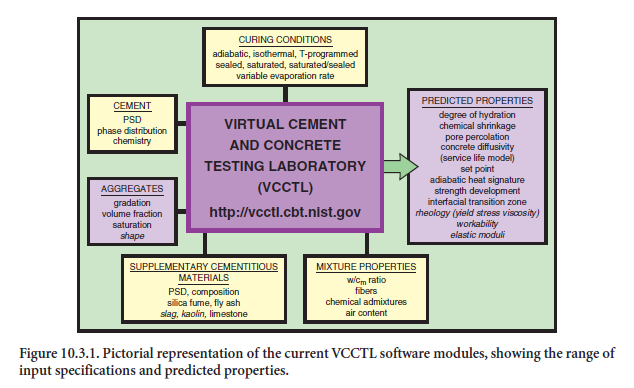
However, it was recognized that there were important gaps between the assumptions (e.g., restricted curing conditions, constraints on starting materials and admixtures, and simplified aggregate shapes) of the models and current industry practice. Born out of the desire to advance the application of computational materials science by making the models able to address an increased number of real issues of concrete practice, the Virtual Cement and Concrete Testing Laboratory (VCCTL) consortium was established in January 2001. The ultimate objective of the VCCTL project is to develop a virtual testing system, using a suite of integrated software modules for designing and testing cement-based materials in a virtual environment, which can accurately predict durability and service life based on detailed knowledge of starting materials, curing conditions, and environmental factors. A pictorial representation of the current modules is provided in Figure 10.3.1. This consortium is a joint NIST/industry effort, and involves a number of leading cement, concrete, aggregates, and admixture companies and associations.
The major advancements needed in the models have been identified, and a joint computational/experimental materials science research program laid out. The major current and continuing research topics of the consortium are:
1. enhancements to the cement hydration and microstructure development model to consider additional supplementary materials such as slag and limestone and the prediction of pore solution ionic concentrations;
2. computation of the elastic properties (elastic modulus, creep, shrinkage) of three-dimen-sional microstructures;
3. experimental measurement and computer modeling of the rheological properties (viscosity, yield stress) of cement-based materials;
4. systematic and comprehensive characterization of materials, including chemical composition, phase identification, and particle size distribution of cement;
5. detailed characterization of aggregate size and shape distributions; and
6. user-friendly scientific visualization of microstructures and dynamic phenomena.
This chapter describes the progress to date with an outline of future research needed. Following these descriptions, three case studies are presented briefly to illustrate the range of issues that have been addressed using the current VCCTL software. Additional details about the consortium itself are provided at the end of the chapter in an appendix.
CEMENT HYDRATION
Research on the NIST digital-image-based three-dimensional model of cement hydration and microstructure development (CEMHYD3D) commenced in 1989. CEMHYD3D (Bentz, 1997; Bentz, 2000) is currently recognized as the most extensive, complete, and robust cement paste microstructure model in the world. As such, the model serves as the core of the Virtual Cement and Concrete Testing Laboratory software (Bentz and Forney, 2000). Starting from the measured particle size distribution (PSD) and a detailed scanning electron micrograph (SEM) and X-ray image set for the cement powder, a starting three-dimensional microstructure of cement (which could include other minerals besides portland cement) particles in water is created. The model cement particles match the phase volume fractions, surface fractions, and correlation structures (which give a measure of phase arrangement) measured on the real 2-D cement powder image set. This microstructure is then submitted to the cement hydration model where the user may specify curing conditions in terms of both thermal (semi-adiabatic/adiabatic, isothermal, temperature-defined) and moisture (saturated, sealed) transfer conditions. As hydration executes in the model, a series of output files is created to monitor specific properties as a function of hydration time or achieved degree of hydration.
Properties monitored include chemical shrinkage, heat release, setting, capillary porosity percolation, pH and other concentrations of species in pore solutions, and strength development.
Current Research
Research has focused on several subtopics: 1) modeling and experimental measurements on systems containing limestone fillers, 2) incorporation of the reactions for slag into CEMHYD3D, and 3) modeling of the pH and ion concentration of the pore solution during hydration. Substantial progress has been made on each of these topics.
Limestone additions to cement are commonplace throughout the world, with the exception of the U.S. In general, small (≤15%) quantities of limestone have no detrimental effects on cement prop-erties and reduce both greenhouse gas emissions, and energy requirements. Additionally, in low w/c ratio concretes, there is insufficient space for all of the cement to hydrate completely, so that some of the cement may be acting as rather expensive reinforcing filler. The VCCTL consortium has been exploring the concept of replacing the coarsest cement particles by limestone fillers in low w/c ratio (≤0.3) concrete, via both computational and experimental research. From the modeling side, reactions for limestone have been added to the CEMHYD3D software. The limestone reacts with aluminates to form a calcium aluminate monocarbonate (AFmc) reaction product, reducing the monosulfoaluminate (AFm) content in the hydrated system (Klemm and Adams, 1990). The consortium has also experimentally examined the concept of replacing the coarsest fraction of the cement particles by limestone filler of a similar size (see Case Study I below for details).
A set of hydration reactions for slag has been incorporated into the latest version of the CEMHYD3D software. To accurately model a given slag, the user must obtain its particle size distribution and oxide composition. The hydration reactions for slag have been developed and partially validated based on materials received from consortium members. The slag reacts with a fraction of the calcium hydroxide produced from the cement hydration to produce a “slag”-gel hydration product containing calcium, silicon, aluminum, magnesium, and possibly sulfate. If the slag contains excess aluminum relative to its magnesium content (with regard to the formation of a hydrotalcite-type phase), the excess aluminate participates in reactions with the calcium sulfate in the cement to form ettringite and monosulfoaluminate (and hydrogarnet when sulfate is not read-ily available). Validation of these reactions has been based on measurements of chemical shrinkage of blended cements (typically 30% slag, 70% cement), measurements of calcium hydroxide production/consumption, and analysis of hydrated microstructures via X-ray diffraction and scanning electron microscopy. To date, good agreement between model predictions and experimental measures has been obtained.
Based on the approach developed and published by Taylor (1987), computation of the alkali (potassium and sodium) concentration in the pore solution during hydration has been added to the CEMHYD3D software. The user must supply information on the total and readily soluble (within 1 h) alkali contents of the cement of interest. The pH prediction module of CEMHYD3D computes the pH of the pore solution along with the concentrations of calcium, potassium, sodium, hydroxide, and sulfate. At early times, while gypsum remains present in the hydrating microstructure, ion concentrations are computed based on the maintenance of equilibrium between the pore solution and the solid phases of calcium hydroxide and gypsum, along with an electroneutrality condition. At later ages, the sulfate concentration is assumed to decrease to zero, and only the equilibrium with calcium hydroxide is maintained. Based on recent experimental data, there is good agreement between model predictions and experimental measurements for both pore solution pH and the concentration of (K+) and (Na+) in solution (unpublished). Furthermore, the first steps have been taken in the CEMHYD3D model to link pH to the reactivity of cement clinker phases and slag or fly ash within CEMHYD3D. Preliminary comparisons to experimental observations suggest that this linkage is a step in the right direction. But the level of agreement between simulation and experiment appears to be system dependent, and further research is in progress to improve the model dependence of reactivity on pH.
Future Hydration Research
The CEMHYD3D component of the VCCTL needs to continue to be developed during the lifetime of the consortium and beyond. This development must take a two-fold path: improving the basic chemical and physical science, including kinetics, of how portland cement hydration is treated under different environmental conditions (temperature, moisture, etc.) and incorporating and/or improving the reactions and interactions of materials like slag, fly ash, metakaolin, and limestone. This will make the model more and more useful for a wider range of materials and hydration conditions. Computational improvements in the model, like improving run time or altering the hydration model to allow the user to increase the model resolution by decreasing the physical dimensions of each voxel, are always being considered, since the computations and the materials science go together to make possible improvements in computational materials science.
ELASTIC PROPERTIES
Predicting the elastic properties of cement-based materials is dependent on three types of informa-tion for each phase: 1) how much of the phase is present, 2) how the phase is arranged in the microstructure, and 3) the values of the elastic moduli of the phase. Items number 1 and 2 are available in the CEMHYD3D output, while item 3 must be measured independently. Cement paste is extraordinarily complex elastically, and this complexity further increases in concrete, as aggregates are added.
A finite element package for computing the elastic moduli of composite materials has been written at NIST and has been available for several years (Garboczi, 1998). The program takes a 3-D digital image of a microstructure, assigns elastic moduli tensors to each voxel according to what material phase is present, and then computes the effective composite linear elastic moduli of the material. This program is highly optimized and has worked successfully for many different material microstructures, including ceramics (Roberts and Garboczi, 2000), metal alloys (Roberts and Garboczi, 1999), closed and open cell foams (Roberts and Garboczi, 2002), gypsum plaster (Meille and Garboczi, 2001), oil-bearing rocks (Arns and others, 2002), and 2-D images of damaged concrete (Stutzman and others, 2001).
Current Research
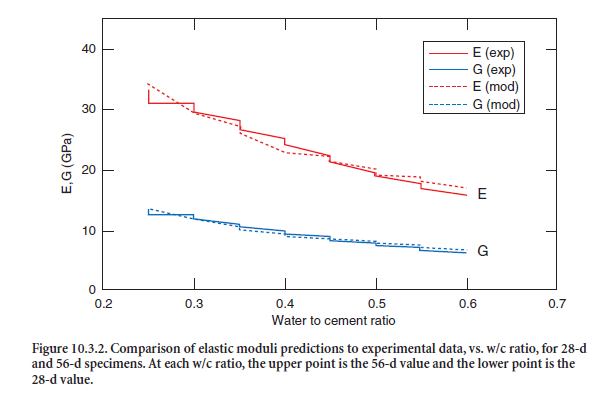
The legacy FORTRAN version of the elasticity model has been rewritten in C and directly incorpo-rated within the VCCTL software system. It can take as input the cement paste microstructure as given by the CEMHYD3D model, and operate on it to compute the cement paste elastic moduli. However, the elastic moduli output is only as good as the phase elastic moduli input. NIST researchers have combed the geological literature to find the available cement/cement paste mineral elastic moduli data. There also have been some recent data reported in the cement litera-ture on cement clinker minerals and on C-S-H. The VCCTL consortium is committed to measure any other individual phase elastic moduli that are needed. Agreement between model and experi-ment is quite reasonable for some later-age, Type 1 specimens that were measured elastically by a member of the consortium. Figure 10.3.2 shows this 28-d and 56-d data (saturated curing), plotted against w/c ratio, for both experimental and model results. The agreement is usually within 5%. Other later-age experimental results for cements of different finenesses also have been predicted well by the model; at equivalent degrees of hydration, fineness does not seem to have a significant effect on elastic moduli.
Future Research
At present, only later age predictions (above about 45% hydration) are accurate using the VCCTL elastic codes. Early-age elastic moduli are more difficult to predict and measure. The low connectivity of voxels between phases at early ages causes large inaccuracies. Using higher-resolution digi-tal representations, as well as modifying the connectivity of the finite element mesh, should help resolve this problem. A step in this direction has been to adapt the legacy FORTRAN code to be executable on parallel computers, allowing much larger systems and therefore much higher resolu-tion systems, to be examined computationally (Bohn, 2003). Other research needed includes efforts to model viscoelastic behavior (creep), and the accurate prediction of concrete elastic moduli (Garboczi and Berryman, 2002). Also, marrying durability simulations to elastic moduli prediction capabilities would allow a hydrated microstructure to be exposed to, for example, leach-ing conditions (the removal of CH) and the elastic moduli of the “degraded” cement paste would then be computed and compared to experiment.
RHEOLOGICAL PROPERTIES
At NIST, there is an ongoing program with the goal of predicting the rheological performance of concrete from its mix design. The prediction is based on several steps:
1. measuring the rheological properties of cement paste to determine the influence of chemical admixtures and supplementary cementitious materials;
2. measuring the rheological properties of mortar to determine the influences of air and sand contents; and
3. predicting concrete properties through computer simulation coupled with experimental rheo-logical measurements on mortar and/or cement paste (Ferraris, 1999a; Ferraris and Martys, 2001; Ferraris, de Larrard, and Martys, 2001a).
This approach is justified by the fact that most chemical admixtures and supplementary cementi-tious materials will have negligible interactions with coarse aggregate. Mortar measurements provide a representative and stable amount of air, as well as a wide range of sand size distributions and shapes. The scientific progression from mortar to concrete then entails only the addition of the coarse aggregates. A novel computational materials science approach allows us to take the rheological properties measured on mortar, add the coarse aggregates with their shape and size distribution, and predict concrete rheological properties. The advantage of this approach is that mortar rheology is much easier and quicker to perform experimentally, and uses much less material than do concrete rheological measurements.
This hierarchical approach obviously needs to be validated at all stages. The rheological properties of cement pastes containing different supplementary cementitious materials (SCM) and high range water-reducing admixtures (HRWRA) were measured and the results were compared to concrete data (Ferraris, Obla, and Hill, 2001). The results showed that the rank of the cement paste mixtures was found to match the concrete performance as characterized by the conventional slump test. A methodology to measure the rheology of mortars was developed and tests are under-way with ideal aggregates (spherical glass beads) in mortar and concrete to validate the model (in collaboration with the Center for Advanced Cement-Based Materials).
The cement paste and mortar measurements are performed using a parallel plate rheometer with different size plates depending on whether cement paste or mortar is to be measured. The materi-als are mixed using a high shear mixer with controlled speed and temperature (Helmuth and others, 1995) to ensure that the material tested experiences conditions typically found in concrete.
The computational materials science model is based on dissipative particle dynamics (DPD) theory (Groot and Warren, 1997; Hoogerbrugge and Koelman, 1992; Koelman and Hoogerbrugge, 1993). This model combines the concepts of cellular automata and molecular dynamics.
The fluid phase is modeled by a collection of discrete particles. These particles may represent an agglomer-ation of molecules or a finite volume of fluid. The DPD algorithm tracks the particle positions at all times. Hoogerbrugge and Koelman (1992) and Koelman and Hoogerbrugge (1993) developed an algorithm for modeling the movement of solid objects of arbitrary shape. A rigid body is represented by “freezing together” a group of particles in the volume occupied by the object, which then move together. This method is being modified for application to the flow of concrete. The shape of real aggregates can be described easily by this method (see Figure 10.3.3 for an example). Therefore, it will be possible, knowing the mortar rheological properties, to “virtually” add the aggregates with the correct shape and size distribution. This will allow the simulation of the rheological properties of a concrete of known composition.
Because this computational approach requires powerful computers beyond the range of those readily available to the cement and concrete community, NIST is building a database that will cata-log the viscosity of concrete with a coarse aggregate defined by its shape and size distribution for various aggregate contents. The VCCTL user may search the database for aggregates similar in shape and size distribution to those being used. Once the mortar properties are measured, the database will provide the relative viscosity1 of the concrete. Obviously, this will allow the reduction of time-consuming and expensive concrete testing by guiding the VCCTL user to the correct concrete composition having the desired rheological properties.
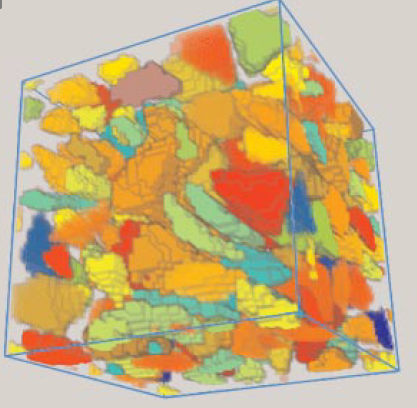
Figure 10.3.3. Showing a model concrete, where the matrix is mortar (transparent in the picture) and there are 45% by volume coarse aggregates. The four different kinds of aggre-gates are similar in size and are taken from real aggregates.
MATERIALS CHARACTERIZATION
Because most of the models used in the VCCTL software are rooted in – and operate upon – the details of cement particle microstructure, an accurate and comprehensive knowledge of the start-ing materials is crucial to the predictive ability of the simulations. Ideally, the most comprehensive model would start from atomic details, and predict macroscopic behavior based solely upon the locations and types of atoms that are present and the environmental conditions. Such a model is far beyond present capabilities. This makes it crucial to experimentally supply many details that the models need so that they may accurately predict macroscopic behavior. This kind of informa-tion is generally in the nature of material characterization. In general, the required analyses are nothing more exotic than those that previously have been applied to cements. However, they must be performed more systematically and thoroughly than they have been in the past. Once this is accomplished, the full predictive power of the models can be utilized.
Prior research using the models has revealed the importance of pinpointing for cement the value of the following variables: 1) volume and mass fractions of each cement phase in the material, including mineral admixtures and gypsum; 2) surface-area fractions of each component of the cement phases, as a measure of how phases are distributed within particles; 3) the particle size distribution of each major cement phase, because particle size is probably the main variable controlling reactivity; and 4) the degree of flocculation or agglomeration among cement particles.
A major thrust of the VCCTL consortium has been to create a “cement database” that catalogs the salient microstructure features of a wide range of cements that are needed as input for the VCCTL models. We have begun to work with ASTM, via committee C01 on Cement, to build these needed measurements into the standards so that this kind of information is routinely available, thus making the models more easily and widely usable.
Particle Size Distribution
Particle size distributions (PSDs) of cements and mineral admixtures are critical to the properties and performance of cement-based materials, as illustrated in the case studies given below. However, a universally recognized standard method for characterizing the size of cement particles does not currently exist (Jillavenkatesa and others, 2001; Hackley and Ferraris, 2001). Standard sieve analysis works fine for most aggregates, but particle size measurement of ultrafine aggregates (diameter <75 µm) suffers from the same lack of a standard method as does cement. Consequently, implementation of different measurement methods for fine particles varies widely. In general, round-robin tests conducted to date have demonstrated a high variability among results, even between participants using instruments based on the same underlying principles. Potential sources of variability in sizing methods include adjustable instrument parameters or material property data required as input parameters and fundamental differences due to the nature of the technique itself. In the latter case, it must be acknowledged that different methods may “sense” a different aspect of the size distribution. For instance, a given method may be sensitive to either particle mass, particle number, or projected surface area. As a result, for a polydisperse system, each method produces a distribution with slightly different weighting. Thus, the “mean” particle diameter values found by different methods are expected to differ.
ASTM Subcommittee C01.25 is currently discussing the development of a standard test for cement PSD. Its approach consists of two steps: 1) define a consensus PSD curve using a standard cement such as NIST Standard Reference Material 114P, and 2) develop standard PSD test procedures.
The first step to achieve these goals was to organize round-robin tests. Two were organized within ASTM (Ferraris, 2002). The results were analyzed and the following conclusions drawn.
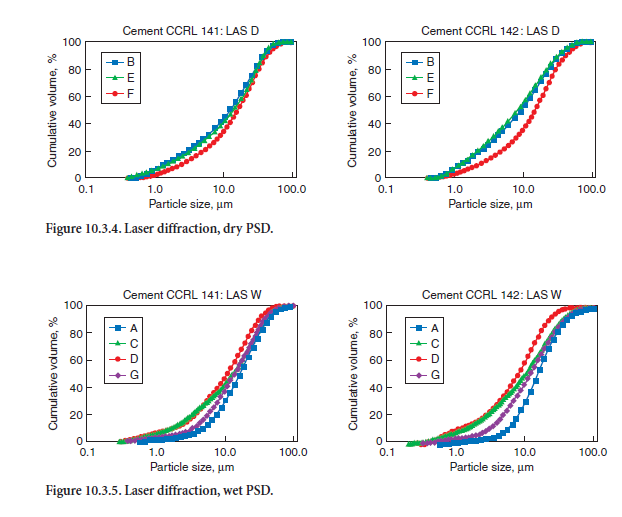
First, by far the most commonly used technique for characterization of cement PSD is laser diffraction, with two dispersion options: wet = the specimen is dispersed in liquid (suspension), and dry = the specimen is dispersed in air (aerosol). The wet technique is currently somewhat more popular than the dry technique and uses various organic solvents in which to suspend the cement particles.
Second, machine parameters used by the various laboratories are not the same and the influence of these parameters is not always clearly understood. These parameters range from the properties of the cement, such as its complex diffraction indices, to the model used to interpret the data measured (Fraunhofer or Mie) and the dispersion medium used (e.g., isopropanol, methanol, or ethanol).
Finally, the dispersion of the PSD obtained with the various methods on the same cement can be very wide, even if the reproducibility of the results by the same operator is very good. For example, Figures 10.3.4 and 10.3.5 show three different results obtained with the laser diffraction dry and wet techniques during the round-robin conducted by the VCCTL members for Cement and Concrete Reference Laboratory (CCRL) (Pielert, 2002) cements 141 and 142 (Ferraris, 2002 – Part II).
NIST is working within the VCCTL consortium and within ASTM to develop a standard test for cement PSD determination by laser diffraction. The collaboration with ASTM will yield at first a “consensus” PSD using NIST cement 114P,a cement that is normally sold to laboratories to cali-brate their Blaine fineness device. The consensus PSD of this cement is being determined by a round-robin test in collaboration with CCRL and ASTM. More than 200 laboratories have been asked to measure the PSD of this cement and a CCRL cement in the context of the existing CCRL proficiency sample program.
NIST will also examine, both experimentally and theoretically, the influence of various parameters on the results obtained from the round-robin tests. This fundamental study, along with the round robin results, will yield the methodology needed to standardize the measurements of cement PSD with this technique. This will allow the VCCTL to more routinely bring cements into its database, since the cement PSD is needed as an input.
SEM/X-Ray Imaging
NIST has pioneered the use of SEM/X-ray imaging for the quantitative characterization of cement powders (Bentz and others, 1999). This analysis produces a 2-D image of the cement powder in which each pixel is identified as one of the major phases of portland cement as shown in Figure 10.3.6. The resultant image can then be further analyzed to determine phase area frac-tions, phase surface area (perimeter) fractions, and phase(s) correlation functions. These measures give an idea of how the particles are arranged next to each other, and how phases are arranged internally within a particle. These characteristics are duplicated in the computer-generated three-dimensional microstructure of cement particles in water. This kind of individ-ual particle characterization allows the model to make accurate predictions, since the accuracy of real results depends on this level of detail, given that this level of detail affects real cement performance.

Figure 10.3.6. Processed 2-D image of CCRL Cement 141: brown is C3S, blue is C2S, gray is C3A, white is C4AF, yellow is calcium sulfate, red is potassium sulfate, pink is periclase, and green is free lime. Image width is 256 µm x 200 µm.
VISUALIZATION
Scientific visualization has always been a critical component of the development of the computa-tional materials science of concrete models. The initial version of the CEMHYD3D model (circa 1989) was developed on a PIXAR imaging computer in the NIST laboratories (the same PIXAR2 that has gone on to create such famous animation movies as Toy Story and A Bug’s Life). Using this machine, the “hydration” could be viewed interactively, greatly expediting algorithm development and debugging activities. This ability to visualize results is crucial for complex models, as models always produce some results, no matter if they are right or wrong. Visualizing results can quickly show if the results obtained are ridiculous, and once the results are correct, visualization helps one to understand the physical significance of large and complex streams of data.
Current Research
As in most areas of computer technology, hardware and software have progressed significantly in recent years. The visualization facilities of the Information Technology Laboratory at NIST continue to be state-of-the-art and heavily utilized in the development of VCCTL models.
One of the newest additions to the visualization facilities at NIST is an Immersive Virtual Reality environment based on a RAVE (Reconfigurable Automatic Virtual Environment) hardware system and appropriate software. The RAVE is a two-wall immersive environment with two 2.44 m x 2.44 m screens flush to the floor and oriented at 90° to form a corner. Using the RAVE environment, the researchers may stand within the cement paste during hydration, to literally “see and feel” what is happening within these complex three-dimensional microstructures.
The visualization also plays an important role in the validation of the algorithms and the correctness of complex systems.
VCCTL CASE STUDIES
To illustrate the power and flexibility of the VCCTL system we have chosen three case studies: 1) Replacement of “Coarse” Cement Particles by Limestone Fillers – Hydration and Strength Development (Bentz and Conway, 2001), 2) Multi-Scale Modeling of the Influence of Condensed Silica Fume Additions on the Diffusivities of Cement Pastes and Concretes (Bentz and others, 2000; Bentz, 2000), and 3) Influence of Cement Particle Size Distribution on Properties (Bentz and Haecker, 1999; Bentz and others, 2001). These examples, as sited below, demonstrate the ability to rapidly explore the multiparameter “material design space” to determine the likely desirability of untried formulations.
Case I.
Replacement of “Coarse” Cement Particles by Limestone
Fillers – Hydration and Strength Development
• VCCTL results have shown that in low w/c ratio systems, the coarser cement particles can be replaced by limestone filler with little reduction in long term compressive strength. A w/c ratio of 0.3 may allow a 15% replacement by volume, and a w/c ratio of 0.25 may allow a 20%replacement.
• Further simulation results suggest that replacing the finest 15% by volume cement particles by limestone (as would be expected when the two materials are interground) will result in a substantial decrease in both early-age and longer-term compressive strengths.
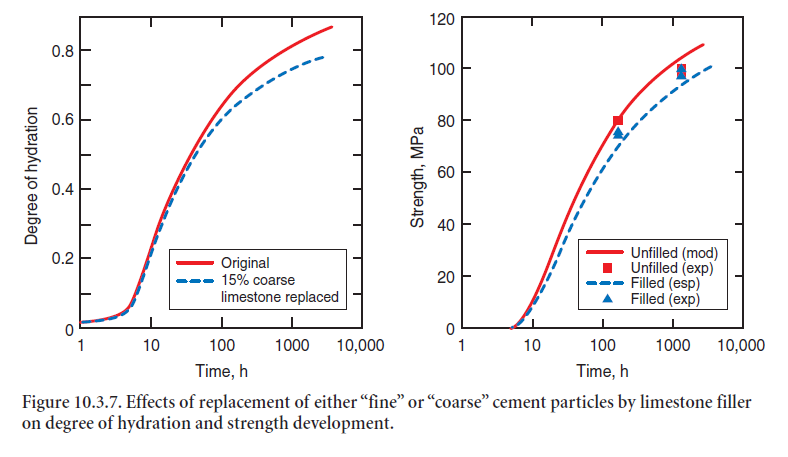
• To experimentally check model results, a high purity limestone and a reference CCRL cement (Pielert, 2002) were classified, separating both materials at a cutoff size of 30 µm, and the PSD was evaluated via laser diffraction. The coarse limestone particles were then blended with the fine cement particles using a V-blender. High performance mortars (w/s=0.3) with and with-out 15% limestone replacement of the coarse cement particles were prepared. The compressive strengths of the mortar cubes were evaluated after 7 days and 56 days of curing in limewater. After 7 days of curing, the system with 15% limestone had a 10% lower compressive strength than the “control” system. But after 56 day of curing, both systems achieved compressive strengths of 99 MPa, demonstrating the viability of replacing coarser cement particles by lime-stone in low w/c ratio mortars and concretes without detracting from the eventual compressive strength (see Figure 10.3.7).
Case II.
Multi-Scale Modeling of the Influence of Condensed Silica
Fume Additions on the Diffusivities of Cement Pastes
• Silica fume influences concrete diffusivity in three ways: 1) by densifying the microstructure of the interfacial transition zones, 2) by reducing the overall capillary porosity for a fixed degree of cement hydration, and 3) by producing a pozzolanic C-S-H (formed from the reac-tion between silica fume and calcium hydroxide) that has an inherent diffusivity to chloride ions that is significantly lower than that of the C-S-H gel formed from conventional cement hydration.
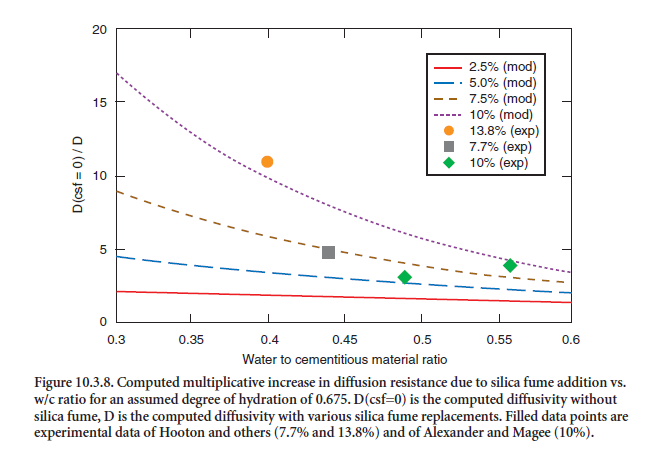
• The influence of silica fume on concrete diffusivity is a strong function of w/c ratio (see Fig.10.3.8). For low w/c ratio concretes, silica fume replacements on the order of 10% may reduce the concrete diffusivity by a factor of 15.
Case III.
Influence of Cement Particle Size Distribution on Properties
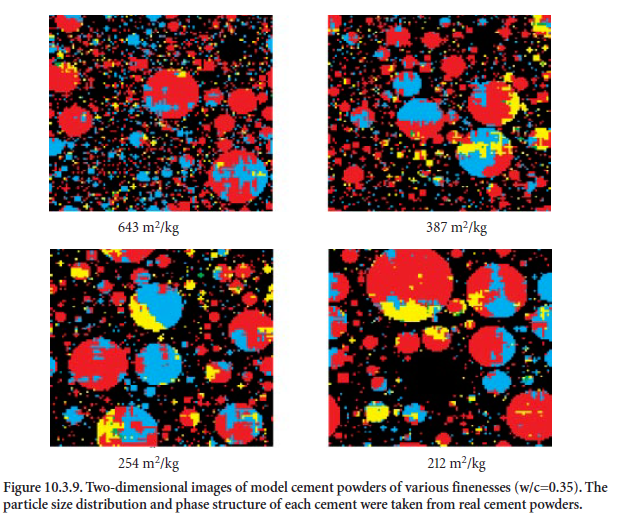
A series of cement paste microstructures with varying cement particle size distributions (and, therefore, varying surface areas) were created and cured using the VCCTL models (see Figure 10.3.9). The hydration performance and various performance properties were computed, with the following results:
• Coarser cements significantly reduce early-age hydration rates and heat release (and strength development), thus may require that more attention be paid to proper curing.
• At equivalent degrees of hydration, diffusivities of “fine” and “coarse” cements are similar.
• Coarser cements significantly reduce autogenous shrinkage.
CONCLUSION
The “virtual cement” concept, as embedded in the Virtual Cement and Concrete Laboratory (VCCTL), cannot, and is not intended to, replace experimental testing. Instead, this chapter and the case studies illustrate that the models can significantly reduce the extent of trial-and-error experimentation by pointing toward those materials that are more likely to be beneficial for a given application. The user may freely explore a wide range of variables as a way of narrowing the search for desired performance.
The models comprising the VCCTL are being upgraded and improved continuously through col-laborations between NIST and its partners in the VCCTL consortium. As the concept of the com-putational materials science of cement gains increasing acceptance within the industry, these kinds of tools are poised to help revolutionize the way cementitious materials are made, tested, and used.
APPENDIX: THE NIST/INDUSTRY VCCTL CONSORTIUM – 2003
Headquartered in the Building and Fire Research Laboratory (BFRL) at the National Institute of Standards and Technology (NIST), the consortium currently consists of two NIST laboratories, BFRL and the Information Technology Laboratory (ITL), and ten industrial members: Cemex, Holcim (US) Inc., the International Center for Aggregate Research (ICAR), the National Ready-Mixed Concrete Association (NRMCA), the Portland Cement Association (PCA), Sika Technology, W. R. Grace & Co. – Conn., Verein Deutscher Zementwerke ev (VDZ), the Association Technique de l’Industrie des Liants Hydraulique, and Master Builders Technologies.
The consortium is governed by the VCCTL consortium oversight board, consisting of one repre-sentative from each of the ten companies and the VCCTL consortium manager from NIST. The oversight board meets two times per year to review research progress and set the scope and agenda of future research. Within each industrial participant’s laboratory, one researcher is assigned to participate in the research programs of the consortium. Once per year, the most recent version of the VCCTL system software is installed on a Linux-based PC at each participating member’s labo-ratory.As of 2003, the latest version of the VCCTL is 3.0. Note that version 1.1 of the public VCCTL system is available online at http://ciks.cbt.nist.gov/vcctl.
Those wishing to learn more about the NIST/Industry VCCTL consortium may access that infor-mation at the VCCTL consortium website at http://www.bfrl.nist.gov/862/vcctl.Alternatively, interested parties may contact the VCCTL Consortium Manager: Dr. Jeffrey W. Bullard, National Institute of Standards and Technology, bullard@nist.gov.
REFERENCES
Note:Many of the citations listed below are available online as an electronic monograph, located at http://ciks.cbt.nist.gov/monograph.In such cases, the location within the monograph is provided.
Arns, C. H.; Knackstedt, M. A.; Pinczewski, W. V.;and Garboczi, E.J., “Computation of Linear Elastic Properties from Microtomographic Images: Methodology and Match to Theory and Experiment,” Journal of Geophysics Research, (67), 1396-1405, 2002.
Bentz, D. P., “Three-Dimensional Computer Simulation of Cement Hydration and Microstructure Development,” Journal of American Ceramic Society, 80 (1), 3-21, 1997, available at Part I, Chapter 4, Section 2(d).
Bentz, D. P., CEMHYD3D: A Three-Dimensional Cement Hydration and Microstructure Development Modelling Package. Version 2.0, NISTIR 6485, U.S. Department of Commerce, April 2000, available at Part I, Appendix I-2.
Bentz, D. P., “Influence of Silica Fume on Diffusivity in Cement-Based Materials. II. Multi-Scale Modeling of Concrete Diffusivity,” Cement and Concrete Research, 30, 1121-1129, 2000, available at Part I, Chapter 7, Section 3.
Bentz, D. P., and Conway, J. T., “Computer Modeling of the Replacement of “Coarse” Cement Particles by Inert Fillers in Low w/c Ratio Concretes: Hydration and Strength,” Cement and Concrete Research, 31 (3), 503-506, 2001, available at Part I, Chapter 4, Section 10.
Bentz, D. P., and Forney, G. F., User’s Guide to the NIST Virtual Cement and Concrete Testing Laboratory. Version 1.0, NISTIR 6583, U.S. Department of Commerce, November 2000, available at Chapter I, Appendix I-3.
Bentz, D. P.; Garboczi, E. J.; Haecker, C. J.; and Jensen, O. M., “Effects of Cement Particle Size Distribution on Performance Properties of Cement-Based Materials,” Cement and Concrete Research, 29, 1663-1671, 1999, available at Part I, Chapter 5, Section 9.
Bentz, D. P., and Haecker, C. J., “An Argument for Using Coarse Cements in High Performance Concretes,” Cement and Concrete Research, 29, 615-618, 1999, at Part I, Chapter 5, Section 8.
Bentz, D. P.; Jensen, O. M.; Coats, A. M.; and Glasser, F. P.,“Influence of Silica Fume on Diffusivity in Cement-Based Materials. I. Experimental and Computer Modeling Studies on Cement Pastes,” Cement and Concrete Research, 30, 953-962, 2000, available at Part I, Chapter 7, Section 3.
Bentz, D. P.; Jensen O. M.; Hansen, K. K.; Oleson, J. F.; Stang, H.; and Haecker, C. J., “Influence of Cement Particle Size Distribution on Early Age Autogenous Strains and Stresses in Cement-Based Materials,” Journal of American Ceramic Society, 84 (1), 129-135, 2001, available at Part I, Chapter 8, Section 2.
Bentz, D. P.; Stutzman, P. E.; Haecker, C. J.; and Remond, S., “SEM/X-ray Imaging of Cement-Based Materials,” 7th Euroseminar on Microscopy of Building Materials, Delft, The Netherlands, 457-466, 1999, available at Part I, Chapter 3, Section 4 and Part I, Chapter 4, Section 1.
Bohn, R. B., and Garboczi, E. J., User Manual for Finite Element and Finite Difference Programs: A Parallel Version of NISTIR-6269, NIST Internal Report, 2003.
Eden, M., in Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and robability Vol. IV, edited by Jerzy Neyman, Univ. of California Press, Berkeley, 1961.
Ferraris, C. F., “Measurement of the rheological properties of cement paste: a New Approach,” Int. RILEM Conf. The role of Admixtures in High Performance Concrete, Eds. J.G. Cabrera and R. Rivera-Villareal, pages 333-342, 1999, available at Part I, Chapter 2, Section 6.
Ferraris, C. F., “Measurement of the Rheological Properties of High Performance Concrete: State of the Art Report,” Jr. NIST Res., 104 (5), 461-478, 1999.
Ferraris, C., and Brower, L., editors, Comparison of concrete rheometers: International tests at LCPC (Nantes, France) in October 2000, NISTIR 6819, U.S. Department of Commerce, September 2001, available at Part I, Chapter 3, Section 8.
Ferraris, C.; de Larrard, F.; and Martys, N., “Fresh Concrete Rheology,” in “Material Science of Concrete VI” Ed. J.P. Skalny, American Ceramic Society, Westerville, OH, 2001, available at Part I, Chapter 2, Section 9.
Ferraris, C., and Martys, N., “De la pâte de ciment au béton: modélisation et mesures expérimen-tales des propriétés rhéologiques,” Proc. Rhéologie Génie Civil et Environment, 36 ème Colloque du Groupe Français de Rhéologie, Marne-la-Vallée (France) October 10-12, pages 226-230, 2001.
Ferraris, C.; Obla, K.; and Hill, R., “The influence of mineral admixtures on the rheology of cement paste and concrete,” Cement and Concrete Research, 31 (2), 245-255, 2001, available at Part I, Chapter 2, Section 7.
Ferraris, C. F.; Hackley, V. A.; Aviles, A. I.; and Buchanan, C. E., “Analysis of the ASTM Round-Robin Test on Particle Size Distribution of Portland Cement: Phase I,” NIST Internal Report 6883, 2002;
“Phase II,” NIST Internal Report 6931, 2002.
Ferraris, C. F. and Martys, N. S., “Relating Fresh Concrete Viscosity Measurements from Different Rheometers,” submitted to ACI Materials Journal, 2003.
Garboczi, E. J., “Finite element and finite difference programs for computing the linear electric and elastic properties of digital images of random materials,” NISTIR 6269, 1998, available at Part II, Chapter 2 in monograph.
Garboczi, E. J.; Bentz, D. P.; and Martys, N. S., “Digital imaging and pore morphology,” in Methods in the Physics of Porous Media, edited by Po-zen Wong, Academic Press, New York, 1999, pages 1-41.
Garboczi, E. J., “Three-dimensional mathematical analysis of particle shape using X-ray tomogra-phy and spherical harmonics: Application to aggregates used in concrete,” Cement and Concrete Research, 32, 1621-1638, 2002.
Garboczi. E. J., and Berryman, J. G., “Elastic moduli of a material containing composite inclusions: Effective medium theory and finite element computations,” Mech. Mater., 33, 455-470, (2001), available at Part II, Chapter 7, Section 7.
Garboczi, E. J., and others, “An Electronic Monograph: Measuring and Modeling the Structure and Properties of Cement-Based Materials,” <http://ciks.cbt.nist.gov/monograph> See especially button for “Downloadable Software,” 1997.
Garboczi, E. J.; Martys, N. S.; Livingston, R. A.; and Saleh, H. S., “Acquiring, analyzing, and using complete three-dimensional aggregate shape information,” in Proceedings of the Ninth Annual Symposium of the International Center for Aggregate Research, Austin, Texas, 2001 (on CD and avail-able at Part I, Chapter 10, Section 3).
Groot, R. D. and Warren, P. B., “Dissipative Particle Dynamics: Bridging the Gap between Atomistic and Mesoscopic Simulation”, J. Chem. Phys., 107, 4423-4435, 1997.
Hackley, V. A., and Ferraris, C. F., The Use of Nomenclature in Dispersion Science and Technology, NIST Special Publication 960-3, 2001.
Helmuth, R.; Hills, L.; Whitting, D.; and Bhattacharja S., Abnormal Concrete Performance in the Presence of Admixtures, RP333, Portland Cement Association, 1995.
Hoogerbrugge, P. J., and Koelman, J. M. V. A., “Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics,” Europhys. Lett., 19,155-160, 1992.
Jennings, H. M., and Johnson, S. K., “Simulation of microstructure development during the hydra-tion of a cement compound,” Journal of American Ceramic Society 69, 790-795, 1986.
Jillavenkatesa, A.; Dapkunas, S. J.; and Lum, L-S. H., Particle Size Characterization, NIST Special Publication 960-1, U.S. Department of Commerce, January 2001.
Koelman, J. M. V. A., and Hoogerbrugge, P. J., “Dynamic Simulations of Hard-Sphere Suspensions Under Steady Shear,” Europhys. Lett., 21, 363-368, 1993.
Klemm, W. A., and Adams, L. D., “An Investigation of the Formation of Carboaluminates,” in Carbonate Additions to Cement, ASTM STP 1064, American Society for Testing and Materials, 1990.
Meakin, P., in Phase Transitions and Critical Phenomena, Vol. 12, edited by C. Domb and J.L. Leibowitz, Academic Press, New York, 1988.
Meille, S., and Garboczi, E. J., “Linear elastic properties of 2-D and 3-D models of porous materials made from elongated objects,” Mod. Sim. Mater. Sci. and Eng., 9, 1-20, 2001, available at Part II, Chapter 7, Section 8.
Pielert, J. H., Cement and Concrete Reference Laboratory (CCRL), http://www.bfrl.nist.gov/862/ccrl/front.htm.
Pryor, Charles, “Aggregates Industry Research Priorities,” Stone Review, November/December 2000, pages 34-38. Available at http://www.nssga.org/calendar/ssgr.htm.
Roberts, A. P., and Garboczi, E. J., “Elastic properties of a tungsten-silver composite by reconstruc-tion and computation,” J. Mech. and Phys. of Solids, 47, 2029-2055, 1999, available at Part II, Chapter 2, Section 3.
Roberts, A. P., and Garboczi, E. J., “Elastic properties of model porous ceramics,” Journal of American Ceramic Society, 83, 3041-3048, 2000, available at Part 2, Chapter 7, Section 4.
Roberts, A. P., and Garboczi, E. J., “Computation of the linear elastic properties of random porous materials with a wide variety of microstructure,” Proc. Roy. Soc. London, 458, 1033-1054, 2002, available at Part II, Chapter 7, Section 9.
Roelfstra, P. E.; Sadouki, H.; and Wittmann, F. H., “Le beton numerique,” Mater. Struct., 18,
327-335, 1985.
Schwartz, L. M., and Banavar, J. R., “Transport properties of disordered continuum systems,” Phys. Rev., B 39, 11965-11969, 1989.
Stutzman, P. E.; Garboczi, E. J.; and Bright, D. S., “Finite element stress computations applied to images of damaged concrete: A possible new diagnostic tool,” Proc. 23rd Int. Conf. on Cement Microscopy, Eds. A. Nisperos and L. Jany, 2001, available at Part I, Chapter 3, Section 6.
Taylor, H.F.W.,Cement Chemistry, Thomas Telford, 1997, and “A Method for Predicting Alkali Ion Concentrations in Cement Pore Solutions,” Adv. Cem. Res., 1 (1), 5-16, 1987.
Wittmann, F. H.; Roelfstra, P. E.; and Sadouki, H., “Simulation and analysis of composite struc-tures,” Mater. Sci. Eng., 68, 239-248, 1984.
Wolfram, S., Theory and Applications of Cellular Automata, World Scientific, Singapore, 1986.
Young, D. A., and Corey, E. M., “Lattice models of biological growth,” Phys. Rev., A 41, 7024-7032, 1990.
Zallen, R., The Physics of Amorphous Solids, Wiley and Sons, New York, 1983.