CLICK HERE TO DOWNLOAD EXCEL SHEETS , BOOKS , MANUALS , OPERATION MANUALS , REFERENCE BOOKS , PROCESS BOOKS

Grinding work index according to Bond

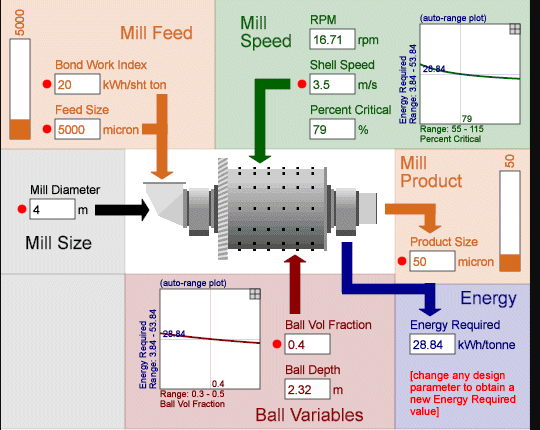
Average  grinding work  index (Wi) by type  of  mate­ rial, according to Bond (see table 6.1.):

The work index (Wi) expresses the kWh required to reduce a short ton of material from theoretically infinite feed size to 80 % passing a square screen opening of 100 microns. The work index values apply to ball mills grinding wet in closed circuit. For dry grinding in closed circuit the work input calculated by Bond’s basic Third Theory equation should be mul­ tiplied by 1.30 (see example 6.3.1.).

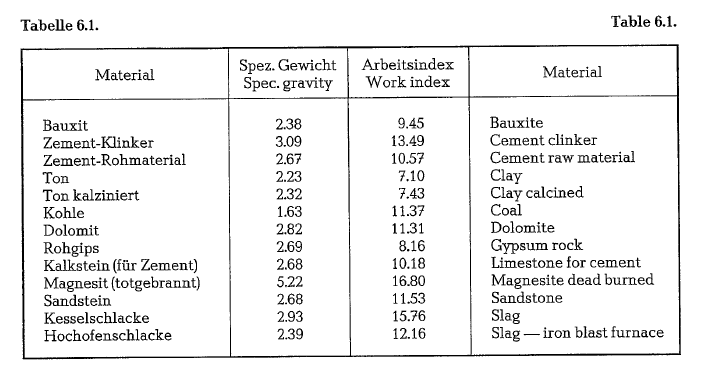
Hardgrove grindability ratings

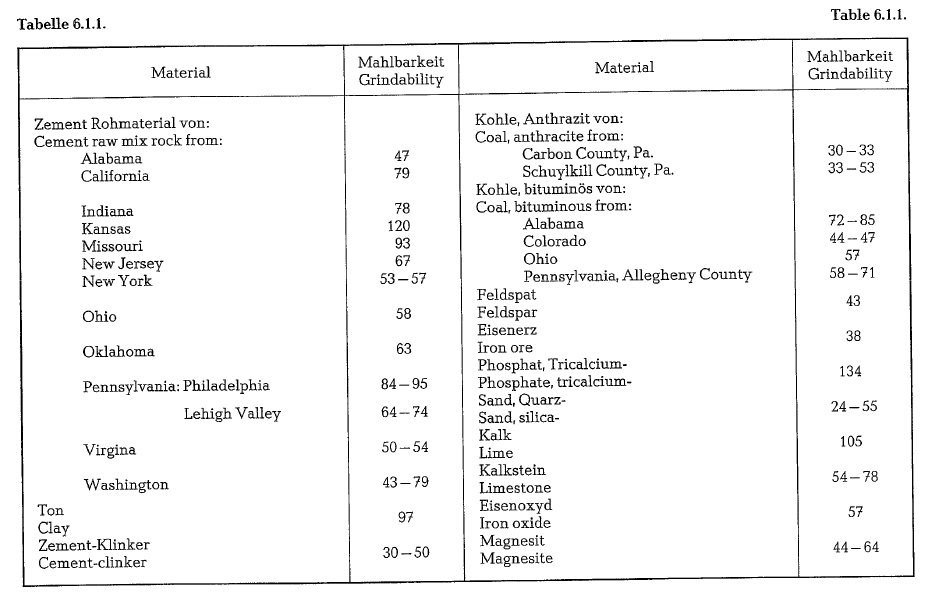
Hardgrove grindability ratings of various materials (grindability increases with magnitude of rating num­ ber) [62]. See table 6.1.1.

Hardgrove grindabilities  (Hg) can be converted to Bond’s Work Indices (Wi), using the following for­mula:

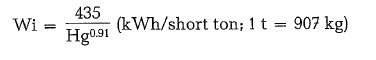
The grinding indices quoted by Bond Tovarov, Hardgrove, etc., result from grinding tests which are performed in special grinding test mills. The test mills are of various sizes and are charged with  different numbers and weights of grinding media. Generally, grinding is performed up to a certain number of mill revolutions, or the test material is ground to a certain fineness, and the consumed energy measured. The results of these tests are grinding indices. A descrip­ tion of all test mills and methods is not within the scope of this discussion; therefore, the following con­ tains only a listing of other grinding test methods:

1. The Lennox-method
2. The Jansey-method
3. The Hertzog-method
4. The Coghill-method
5. The Mackson-Kaden-method
6. The ASTM-method
7. The Allis-Chalmers-method
8. The Papadakis-method
9. The Gross-Zimmerley-method
10. The Zeisel-method, which is almost the only method used in Germany.

The Starke-formula

The Starke-formula [63] determines the optimum ratio of the initial particle size to the grinding ball size and suggests that a grinding mill is most efficient in prod­ ucing surface when the ratio of

The optimum value of this ratio depends on the phys­ical characteristics of the material to be ground.

Slegten [64] says that in the range of coarse grinding, different sizes of grinding balls yield better grinding results than balls of the same diameter. However, in the range of fine grinding better grinding results are obtained with grinding balls of the same size.

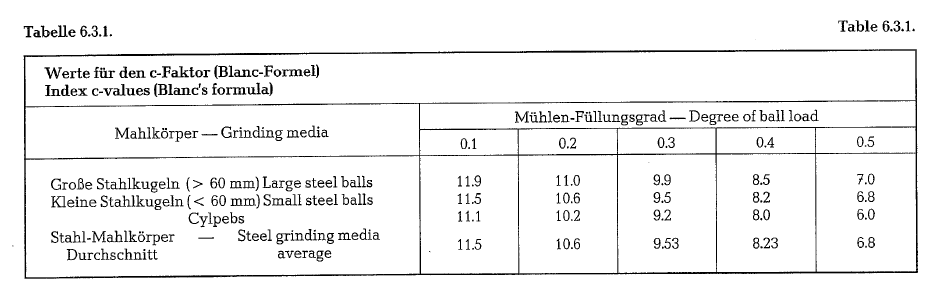
Ball mill power demand

The approximate power demand of a ball mill with the proper mill speed and an optimum load of grinding media, can be derived from the following empirical formula:

According to  Bond’s  Third  Theory  of  comminu­tion; the basic Third Theory equation is:

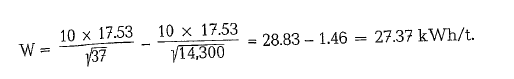
27.37 x 1.113 (fine product factor, see below) = 30.46 Cement production: 54.5 t/h x 30.46 kWh = 1660 kW x 1.341 = 2226 HP are required for the finish mill drive; the actual motor size depends  upon the mechanical losses of the mill drive arrangement.

Fine product factor (to Bond’s equation); should the product size, P, be smaller than 70 microns, then the work input is multiplied by the following empirical adjustment factor A1, which equals

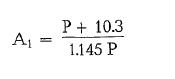
Specific surface and particle size {to Bond’s equation)

Table 6.4.1. contains an approximate comparison of the 80 0/o passing size in microns to the correspond­ ing specific surface (according to Wagner and Blaine), and also the fine product  factor A1 for the  product particle size P. The ratio of the Wagner-surface to the Blaine-surface = 1 : 1.8.

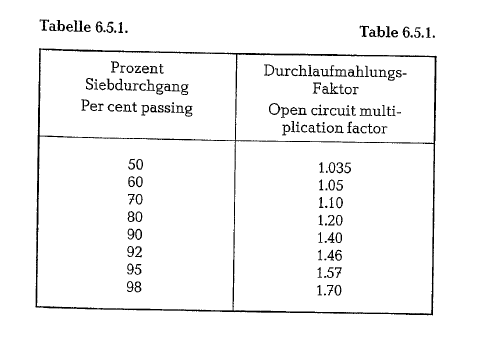
Conversion to open-circuit grinding

Conversion to open-circuit grinding, either wet  or dry, is done  by multiplying the closed circuit work input W (Bond’s equation), by an open circuit multi­ plication factor. This factor varies with per cent pass­ing. Some  open-circuit  multiplication  factors  for various reference percentages passing are listed in table 6.5.1.

Ball mill capacity

According to Tovarov; Tovarov’s formula [41] for the determination of ball mill capacity is:

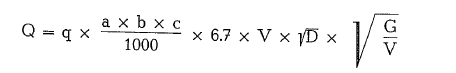
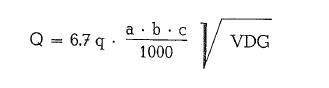
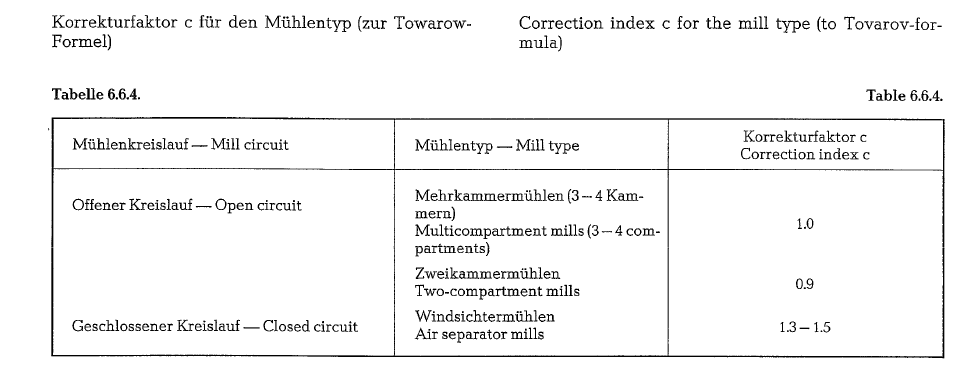
The Tovarov grindability index is used to determine the influence of materials on the cement clinker grinding capacity of a mill; the basis is rotary kiln clinker with a defined grindability index of a = 1. According to this, a mill grinding 30 t/h clinker, will grind 30 x 1.40 = 42 t/h of marl or 30 x 0.6 = 18 t/h of silica sand.

The grindability index of rotary kiln clinker itself varies with its mineralogical composition  and depends above all upon the dicalcium silicate-content of the clinker; the higher the percentage of dicalcium silicate, the more difficult it is to grind the clinker.

Table 6.6.2. [66] contains various values of the grinda­ bility index, a, for rotary kiln clinker, as a function of the dicalcium silicate content (for use in the Tovarov formula).

Storage time also influences the grindabity of the clinker. Fresh clinker is harder to grind than clinker which has been stored 2 or 3 weeks. Depending upon the storage time, the grindability index a varies within the limits of 0.9 to 1.15.

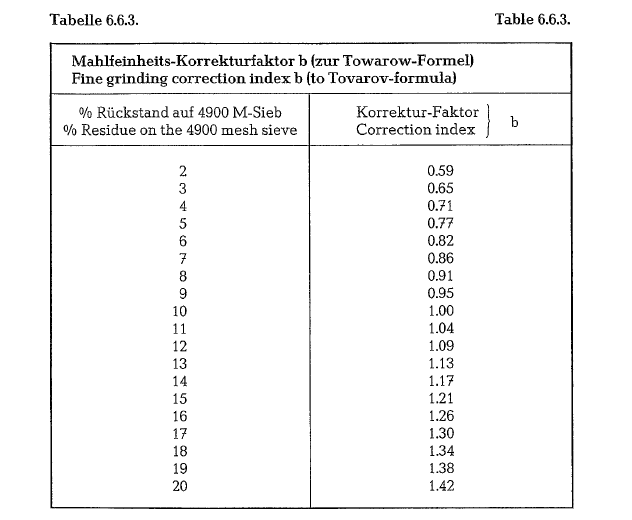
The fine grinding correction index b depends upon the residue of the ground material on the 4900 mesh/cm2-sieve, and was defined as b = 1 corresponding to a residue of  10 %. Table 6.6.3. contains various values of b, as a function of the sieve residue.

In order to evaluate the grinding work of tube mills Jacob [67] developed equations for the co-called capacity value and for the mill throughput. The capa­ city value refers to the Blaine-surface (cm2/gram) of the product because  it is the best reference for grind­ ing work. For grinding cement clinker the specific throughput expressed as kg/kWh was derived from practical grindability tests; this throughput  was found to   be   40 kg/kWh   at   a   specific   Blaine-surface   of 2650 cm2/gram (see Fig. 6.1.). An inner grinding path diameter of DMb = 1 was assumed as a reference point for the volume of the grinding space; to this reference point a throughput of 0.2 t/m3 · h was assigned.

To estimate the specific throughput according  to the grindability curve, the Blaine-number of the finished product is used. The specific reference  throughput of 40 kg/kWh is then divided by the specific throughput a (see formula), drawn from the grindability curve. Using the formula for the capacity value Mz, the grinding work of tube mills of any type and size can be determined. The optimum capacity  value  is  100 and can be obtained when the specific throughput of the mill is of the same quantity as the specific throughput according to the grindability curve at the same Blaine-number, and if the mill throughput satis­ fies the conditions of Jacob’s throughput formula.

Jacob’s mill formulas are:

Thus both mills have the same Jacob’s  capacity value and consequently perform the same grind­ ing work. This applies generally to open as well as to closed circuit grinding.

Problem 6.6.3.

The same mill as quoted in problem 6.6.2.  should grind rotary kiln clinker to cement with a Blaine-sur­ face of 3000 cm2/g. According to  the  grindability curve shown above, this Blaine-number is equal to a specific throughput of 35 kg/kWh. The grinding work should correspond to a capacity value of  100.

Estimate:

1. the throughput, t/h
2. the power demand, kW
3. the power demand of the motor, kW

Power demand of various grinding systems